Grabidade
La grabidade ye ua de las quatro fuorças fundamentales de la natureza (junto cula fuorça fuorte, eiletromagnetismo i fuorça fraca) an que oubjetos cun massa eisercen atraçon uns subre ls outros.[1] Classicamente, ye çcrita pula lhei de Newton de la grabitaçon ounibersal. Fui antendida purmeiramente de modo matemático pul físico anglés Isaac Newton i zambolbida i studada al lhongo de ls anhos.
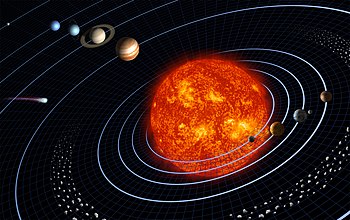
De l punto de bista prático, l'atraçon grabitacional de la Tierra cunfire peso als oubjetos i faç cun que caian al suolo quando son soltos ne l'aire (cumo l'atraçon ye mútua, la Tierra tamien se mobe an direçon als oubjetos, mas solo por ua ínfima fraçon). Ademales, la grabitaçon ye l motibo pul qual la Tierra, l Sol i outros cuorpos celhestriales eisisten: sin eilha, la matéria nun se tenerie aglutinado para formar aqueilhes cuorpos i la bida cumo a antendemos nó tenerie surgido. La grabidade tamien ye respunsable por manter la Tierra i ls outros planetas an sues respetibas órbitas an torno de l Sol i la Lhuna an órbita an buolta de la Tierra, bien cumo pula formaçon de las marés i por muitos outros fenómenos naturales.
Grabitaçon
eiditarGrabitaçon ye la fuorça de atraçon qu'eisiste antre todas las partículas cun massa ne l ouniberso.
La grabitaçon ye respunsable por prender oubjetos a la superfice de planetas i, d'acuordo culas lheis de l mobimiento de Newton, ye respunsable por manter oubjetos an órbita an torno uns de ls outros.
La grabidade faç mui mais de l que simplesmente segurar-mos a las nuossas cadeiras. Fui Isaac Newton quien la reconheciu. Newton screbiu nua de las sues mimórias que na altura an que staba a tentar cumprender l que mantenie la Lhuna ne l cielo biu ua maçana caer ne l sou maçanal, i cumprendiu que la Lhuna nun staba suspensa ne l cielo mas si que caía cuntinamente, cumo se fusse ua bola de canhon que fusse çparada cun tanta belocidade que nunca atinge l suolo por este tamien "caer" debido a la curbatura de la Tierra.
Segundo la terceira lhei de Newton, qualesquiera dous oubjetos eisercen ua atraçon grabitacional un subre l'outro d'eigual balor i sentido ouposto.
Lhei de Newton de Grabitaçon Ounibersal
eiditarPouco se sabie subre grabitaçon até l seclo XVII, pus acraditaba-se que lheis defrentes gobernában ls cielos i la Tierra. La fuorça que mantenie la Lhuna pendurada ne l cielo nada tenie a ber cula fuorça que ne ls mantén presos a la Tierra. Isaac Newton fui l purmeiro a pensar na heipótese de las dues fuorças possuíren las mesmas naturezas; até anton, habie solo la teorie magnetista de Johannes Kepler, que dezie qu'era l magnetismo que fazie ls planetas orbitáren l Sol
Newton splica, "Todos ls oubjetos ne l Ouniberso atraen todos ls outros oubjetos cun ua fuorça direcionada al lhongo de la lhinha que passa puls centros de ls dous oubjetos, i que ye proporcional al perduto de las sues massas i ambersamente proporcional al quadrado de la separaçon antre ls dous oubjetos."
Newton acabou por publicar la sue, inda hoije famosa, lhei de la grabitaçon ounibersal, ne l sou Principia Mathematica, cumo:
adonde:
- F = fuorça grabitacional antre dous oubjetos
- m1 = massa de l purmeiro oubjeto
- m2 = massa de l segundo oubjeto
- r = çtáncia antre ls centros de massa de ls oubjetos
- G = custante ounibersal de la grabitaçon
La fuorça d'atraçon antre dous oubjetos ye chamada de peso.
Rigorosamente falando, esta lhei aplica-se solo a oubjetos semelhantes a puntos. Se ls oubjetos possuíren stenson spacial, la berdadeira fuorça terá de ser ancontrada pula antegraçon de las fuorças antre ls bários puntos. Por outro lhado, puode probar-se que para un oubjeto cun ua çtribuiçon de massa sfericamente simétrica, l'antegral resulta na mesma atraçon grabitacional que tenerie se fusse ua massa pontual.
Fui este oustaclo que lhebou Newton a adiar por bários anhos la publicaçon de la sue teorie, yá qu'el nun cunseguia amostrar que la grabitaçon eisercida pula Tierra subre un cuorpo a la sue superfice era la mesma cumo se to la massa de la Tierra stubisse cuncentrada an sou centro.[2]
Forma Betorial
eiditarLa forma arriba çcrita ye ua berson simplificada. Eilha ye spressa mais propiamente pula forma que segue, la qual ye betorialmente cumpleta. (Todas las grandezas an negrito repersentan grandezas betoriales)
adonde:
- ye la fuorça eisercida an por
- i son las massas
- ison ls betores posiçon de las dues massas respetibas
- ye la custante grabitacional
Pa la fuorça na massa dous, simplesmente tome l'ouposto de l betor
La percipal defrença antre las dues formulaçones ye que la segunda forma usa la defrença na posiçon para custruir un betor qu'apunta dua massa pa l'outra, i de seguida debede l betor pul sou módulo para eibitar que mude la magnitude de la fuorça.
Aceleraçon de la grabidade
eiditarPara saber l'aceleraçon de la grabidade dun astro ó cuorpo, la fórmula matemática ye parecida:
adonde:
- A = aceleraçon de la grabidade
- m = massa de l'astro
- r = çtáncia de l centro de l'oubjeto
- G = custante ounibersal de la grabitaçon
Cumparaçon cula fuorça eiletromagnética
eiditarL'atraçon grabitacional de ls protons ye aprossimadamente un fator 1036 mais fraco que la repulson eiletromagnética. Este fator ye andependiente de çtáncia, porque ambas las fuorças son ambersamente proporcionales al quadrado de la çtáncia. Esso senefica que, nua baláncia atómica, la grabidade mútua ye çprezable. Mas, la fuorça percipal antre ls oubjetos quemuns i la Tierra i antre cuorpos celhestriales ye la grabidade, quando pul menos un deilhes ye eiletricamente neutro, ó quaije. Assi i to se an ambos ls cuorpos houbisse un scesso ó déficit de único eiletron para cada 1018 protones esto yá serie suficiente para cancelar la grabidade (ó ne l causo dun scesso nun i un déficit ne l'outro: duplicar l'atraçon).
La relatiba fraqueza de la grabidade puode ser demunstrada cun un pequeinho ímana, que bai atraindo para cima pedaços de fierro pousados ne l suolo. L minúsclo ímana cunsegue anular la fuorça grabitacional de la Tierra anteira.
La grabidade ye pequeinha, a menos qu'un de ls dous cuorpos seia grande, mas la pequeinha fuorça grabitacional eisercida por cuorpos de tamanho ourdinairo puode ser demunstrada cun razoable facelidade por spriéncias cumo la de la barra de torçon de Cabendish.
Sistema Outo-Grabitacional
eiditarUn sistema outo-grabitacional ye un sistema de massas mantidas juntas pula sue grabidade mútua. Un eisemplo de tal ye ua streilha.
Stória
eiditarNaide ten certeza se l cunto subre Newton i la maçana ye berídico, mas l pensar, cun certeza, ten sou balor. Naide antes del ousou cuntrariar Aristóteles i dezir que la mesma fuorça qu'atrai ua maçana pa l suolo mantén la Lhuna, la Tierra, i todos ls planetas an sues órbitas.
Newton nun fui l único a fazer cuntribuiçones seneficatibas pa l'antendimiento de la grabidade. Antes del, Galileu Galilei corrigiu ua noçon quemun, partida de l mesmo Aristóteles, de qu'oubjetos de massas defrentes caen cun belocidades defrentes. Para Aristóteles, simplesmente fazie sentido qu'oubjetos de massas defrentes demorassen tiempos defrentes a caer de la mesma altura i esso era l bastante para el. Galileu, inda assi, tentou de fato lhançar oubjetos de massas defrentes al mesmo tiempo i de la mesma altura. Çprezando las defrenças debido al arrastre de l'aire, Galileu ouserbou que todas las massas acelerában eigualmente. Podemos deduzir esso usando la Segunda Lhei de Newton, . Se cunsidrarmos dous cuorpos cun massas i mui menores de l que massa de a tierra , oubtemos las eiquaçones:
Debedindo la purmeira eiquaçon por i la segunda por oubtemos:
ó seia, .
La teorie giral de la grabidade de Einstein
eiditarLa formulaçon de la grabidade por Newton ye bastante percisa pa la maiorie de ls propósitos práticos. Eesisten, inda assi, alguns porblemas:
- Assume qu'altaraçones na fuorça grabitacional son trasmitidas anstantaneamente quando la posiçon de ls cuorpos grabitantes muda. Mas, esto cuntradiç l fato qu'eisiste ua belocidade lhemite la que puoden ser trasmitidos ls senhales (belocidade de la luç ne l bácuo).
- L pressuposto de spácio i tiempo absolutos cuntradiç la teorie de relatebidade special de Einstein.
- Prediç que la luç ye zbiada pula grabidade solo metade de l que ye afetabamente ouserbado.
- Nun splica óndias grabitacionales ó buracos negros,
- D'acuordo cula grabidade newtoniana (cun trasmisson anstantánea de fuorça grabitacional), se l Ouniberso ye euclidiano, stático, de densidade uniforme an média positiba i anfenito, la fuorça grabitacional total nun punto ye ua série dibergente. Por outras palabras, la grabidade newtoniana ye ancumpatible cun un Ouniberso cun estas propiadades.
Pa l purmeiro destes porblemas, Einstein zambolbiu ua nuoba teorie de la grabidade chamada relatebidade giral, publicada an 1915. Esta teorie prediç que la persença de matéria "distorce" l'ambiente de spácio-tiempo lhocal, fazendo cun que lhinhas aparentemente "retas" ne l spácio i ne l tiempo téngan caratelísticas que son normalmente associadas la lhinha "rebuoltas".
Ambora la relatebidade giral seia, anquanto teorie, mais percisa que la lhei de Newton, requer tamien un formalismo matemático seneficatibamente mais cumplexo. An beç de çcrebir l'eifeito de grabitaçon cumo ua "fuorça", Einstein antroduziu l cunceito de spácio-tiempo curbo, adonde ls cuorpos se moben al lhongo de trajetórias rebuoltas.
La teorie de la relatebidade de Einstein prediç que la belocidade de la grabidade (defenida cumo la belocidade la que mudanças na lhocalizaçon dua massa son propagadas l'outras massas) debe ser cunsistente cula belocidade de la luç. An 2002, la spriéncia de Fomalont-Kopeikin porduziu mediçones de la belocidade de la grabidade que correspondírun l'esta prediçon. Inda assi, esta spriéncia inda nun sofriu un porcesso amplo de rebison puls pares, i stá a ancontrar ceticismo por parte de ls qu'afirman que Fomalont-Kopeikin nun fizo mais de l que medir la belocidade de la luç dua forma antrincada.
Custante cosmológica
eiditarAl screbir l'eiquaçon de la grabitaçon segundo la Relatebidade Giral, Einstein antroduziu un termo chamado de custante cosmológica, para que la soluçon de las eiquaçones fússen un ouniberso stático. Al tomar coincimiento de la spanson de l Ouniberso, Einstein remobiu este termo, dezindo qu'este fui l sou maior erro.
Esta custante ten sido oubjeto de studo, para splicar l período coincido cumo anflaçon cósmica. L'eifeito de la custante cosmológica serie análogo a ua "grabidade repulsiba", i, ne l tiempo persente, causarie ua aceleraçon de la spanson de l Ouniberso.
Macánica quántica
eiditarLa fuorça de la grabidade ye, de las quatro fuorças de la natureza, la única qu'oustinadamente se recusa a ser quantizada (las outras trés - l eiletromagnetismo, la fuorça fuorte i la fuorça fraca puoden ser quantizadas). Quantizaçon senefica que la fuorça puode ser medida an partes çcretas que nun puoden ser diminuídas an tamanho, nun amportando l qu'acunteça; altarnatibamente, essa anteraçon grabitacional ye trasmitida por partículas chamadas grabitons. Cientistas ténen studado subre l grabiton por anhos, mas ténen tenido solo frustraçones nas sues buscas para ancontrar ua cunsistente teorie quántica subre esso. Muitos acraditan que la Teorie de cuordas alcançará l grande oubjetibo d'ounir Relatebidade Giral i Macánica Quántica, mas essa promessa inda nun se rializou.
Aplicaçones Speciales de Grabidade
eiditarUa defrença d'altura puode possibelitar ua útele presson nun lhíquido, cumo ne l causo de l goteijamiento antrabenoso (Antrabenous Drip) i la Torre de Auga.
La massa suspensa por un cabo atrabeç dua polia possibelita ua tenson custante ne l cabo, ancluindo ne l'outro lhado de la polia.
Cumparaçon de la fuorça de la grabidade an defrentes planetas
eiditarL'aceleraçon debido a la grabidade a la superfice de la Tierra ye 9,80665 m/s² (l balor rial barie lhigeiramente al lhongo de la superfice de la Tierra; ber g para mais detalhes). Esta medida ye coincida cumo gm, gi, g0, ó simplesmente g. La lhista que se segue apersenta la fuorça de la grabidade (an múltiplos de g) na superfice de ls planetas de l Sistema Solar[Nota 1].
| Marcúrio | 0.376 | |
| Bénus | 0.903 | |
| Tierra | 1 | |
| Marte | 0.38 | |
| Júpiter[Nota 2] | 2.34 | |
| Saturno[Nota 2] | 1.16 | |
| Ourano[Nota 2] | 1.15 | |
| Netuno[Nota 2] | 1.19 |
- ↑ Para eifeito de cumparaçon, an Pluton, la fuorça de la grabidade ye 0.066
- ↑ 2,0 2,1 2,2 2,3 Ls gigantes gasosos (Júpiter, Saturno, Ourano i Netuno) nun ten ua superfice sólida ouserbable. Nesse causo fui cunsidrado pa l cálclo la çtáncia al centro de l planeta adonde la presson atmosférica ye de 1 atn, eigual a la presson atmosférica al nible de l mar na Tierra
Ne ls cuorpos sféricos, la grabidade superficial an m/s² ye 2.8 × 10−10 bezes l centeilha an m bezes la densidade média an kg/m³.
Outras teories grabitacionales
eiditar- Teorie aristotélica de la grabitaçon
- Teorie grabitacional de Le Sage (1784) perpuosta por Georges-Lhouis Le Sage
- Teorie de grabitaçon de Nordströn (1912, 1913)
- Teorie de grabitaçon de Whitehead (1922)
- Teorie de Branes–Dicke(1961)
- Grabidade anduzida (1967), ua perpuosta de Andrei Sakharob segundo la qual la teorie de la relatebidade giral tenerie ourige na teorie quántica de campos
- Na dinámica newtoniana modificada (MOND) (1981), Mordehai Milgron propone ua modificaçon na segunda lhei de Newton para pequeinhas aceleraçones.
- Teories grabitacionales de cosmologie d'outocriaçon, de G.La. Barber, ne l qual la teorie de Branes-Dicke ye modificada para permitir la criaçon an massa.
- Teorie de la grabitaçon assimétrica (NGT) (1994) de John Moffat
- Grabidade tensor-betor-scalar (TeBeS) (2004), ua modificaçon relatibística de MOND por Jacob Bekenstein
Lhigaçones sternas
eiditar- L que ye grabidade (an pertués) - Rebista Nuoba Scuola
Ber tamien
eiditarRefréncias
- ↑ Does Grabity Trable at the Sped of Lhight?[lhigaçon einatiba], UCR Mathematics. 1998. Retriebed 3 July 2008
- ↑ La story of astronomy, outor Anton Pannekoek
